Svolgiamo insieme Come svolgere questo integrale col teorema dei residui?
- Autore discussione giammy677
- Data d'inizio
Ho trovato difficoltà a risolverlo. Io mi sono trovato per la curva di integrazione |z|=5pi. Ma tu come hai provato a calcolare il modulo di z?
Io so come svolgere integrali col teorema dei residui, solo che quelli che ho fatto finora mi davano direttamente gli estremi di integrazione in modo che poi io possa capire quale metodo scegliere per risolvere.
In questo caso, in tutta onestà, non so proprio come calcolarmi gli estremi di integrazione. Sapresti aiutarmi?
In questo caso ti da una curva. Risolvendo quella equazione e trovando il modulo di z hai trovato un curva che è una circonferenza di raggio |z|.
Poi vedi quali sono i poli della funzione da integrare e, per risolvere l'integrale, consideri solo i poli interni alla curva che hai trovato prima.
Poi per quanto riguarda il semplice calcolo di |z| e quindi del raggio della circonferenza, io ho trovato |z|=5pi. Ma non sono sicuro che sia il risultato esatto.
Poi vedi quali sono i poli della funzione da integrare e, per risolvere l'integrale, consideri solo i poli interni alla curva che hai trovato prima.
Poi per quanto riguarda il semplice calcolo di |z| e quindi del raggio della circonferenza, io ho trovato |z|=5pi. Ma non sono sicuro che sia il risultato esatto.
Ok, ho capito. Saresti così gentile da spiegarmi solo come definirmi la circonferenza da considerare? Non dovrei considerare i due diversi casi del valore assoluto?
Il caso più semplice che ti possa capitare è:
|z|=n
in questo caso significa che il modulo di z, che non è altro che un vettore nel piano complesso, ha una lunghezza pari a n. Quindi fissato il modulo, al variare dell'argomento di z hai disegnato una circonferenza di raggio n.
Per il tuo esercizio il ragionamento è lo stesso, ma avendo:
|z-pi|=4pi
bisogna ritrovarsi nella situazione di prima di |z|=n.
Ho provato a risolvere questa equazione che sta nel tuo esercizio. Ho considerato:
z = a+ib
Sostituendo:
| a +ib - pi| = 4pi -----> |(a-pi) +ib| = 4pi
Calcolando il modulo che è la radice dei quadrati di (a-pi) e di (b). TI trovi:
[(a-pi)^2] + [b^2] =(4pi)^2
Questa è l'equazione di una circonferenza di raggio 4pi e di centro (pi, 0).
Quindi adesso bisogna semplicemente fare l'integrale con i residui nel modo classico. Ossia la somma dei residui. Ma questa volta si fa la somma dei soli residui interni alla circonferenza. Ti allego la foto dei passaggi della equazione perchè non riuscendo a formattare le formule non si capisce nulla.
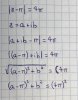
|z|=n
in questo caso significa che il modulo di z, che non è altro che un vettore nel piano complesso, ha una lunghezza pari a n. Quindi fissato il modulo, al variare dell'argomento di z hai disegnato una circonferenza di raggio n.
Per il tuo esercizio il ragionamento è lo stesso, ma avendo:
|z-pi|=4pi
bisogna ritrovarsi nella situazione di prima di |z|=n.
Ho provato a risolvere questa equazione che sta nel tuo esercizio. Ho considerato:
z = a+ib
Sostituendo:
| a +ib - pi| = 4pi -----> |(a-pi) +ib| = 4pi
Calcolando il modulo che è la radice dei quadrati di (a-pi) e di (b). TI trovi:
[(a-pi)^2] + [b^2] =(4pi)^2
Questa è l'equazione di una circonferenza di raggio 4pi e di centro (pi, 0).
Quindi adesso bisogna semplicemente fare l'integrale con i residui nel modo classico. Ossia la somma dei residui. Ma questa volta si fa la somma dei soli residui interni alla circonferenza. Ti allego la foto dei passaggi della equazione perchè non riuscendo a formattare le formule non si capisce nulla.
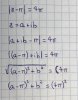
Grazie mille della risposta. In realtà ho trovato un eserciziario che svolge questa tipologia di esercizi in maniera molto più semplice. Te la allego, spero che sia corretta.
Trovi esercizi simili al mio a pagina 8 e poi le soluzioni a pagina 26.
Ti allego anche, in base a questo eserciziario, come ho svolto io l’esercizio.Se vuoi fammi sapere che ne pensi.
Trovi esercizi simili al mio a pagina 8 e poi le soluzioni a pagina 26.
Google Drive: Sign-in
Access Google Drive with a Google account (for personal use) or Google Workspace account (for business use).
drive.google.com
Ti allego anche, in base a questo eserciziario, come ho svolto io l’esercizio.Se vuoi fammi sapere che ne pensi.
Allegati
Vabbeh io avevo scritto tutto per far capire il ragionamento. Alla fine come hai fatto tu è semplicemente che l'equazione:
|z-n| = m
significa che il cerchio è centrato in -n e ha raggio m. Volevo solo far capire come si arriva a questa conclusione.
Comunque ho visto anche il tuo esercizio e noto che però hai scritto |z+pi| = 4pi, e di conseguenza hai trovato una circonferenza di centro -pi. Ma tu mi avevi detto che l'equazione era |z-pi| = 4pi. Per questo io ho calcolato che il centro è (pi) e non (-pi).
|z-n| = m
significa che il cerchio è centrato in -n e ha raggio m. Volevo solo far capire come si arriva a questa conclusione.
Comunque ho visto anche il tuo esercizio e noto che però hai scritto |z+pi| = 4pi, e di conseguenza hai trovato una circonferenza di centro -pi. Ma tu mi avevi detto che l'equazione era |z-pi| = 4pi. Per questo io ho calcolato che il centro è (pi) e non (-pi).
Certo, sei stato gentilissimo infatti. Grazie mille davvero per l’aiuto. E si, l’esercizio che ti avevo chiesto era col - quindi il tuo ragionamento è giustissimo.
grazie mille davvero
