Traccia Gelli 15/10/15
- Autore discussione Fabio
- Data d'inizio
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Qualcuno è riuscito a svolgere gli esercizi?
Io posto le soluzioni 3a e 3b
Il dominio D è il seguente:

a) alfa = 4 / (2 + pi)
b) fx (x) = [4x / (2+pi) ] + [ 4 radice(1-x^2) / (2+pi) ]
fy (y) = 4/(2+pi) * [1 - y + radice(1-y^2)]
il punto c) non riesco a capire il dominio. Si dovrebbe intersecare il dominio D con un dominio in cui x>|y| ma graficamente non riesco a vederlo. Mi sono aiutato con wolfram ma non capisco come viene fuori il grafico .-. L'area da calcolare è quella delimitata dal rosso.
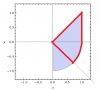
Io posto le soluzioni 3a e 3b
Il dominio D è il seguente:

a) alfa = 4 / (2 + pi)
b) fx (x) = [4x / (2+pi) ] + [ 4 radice(1-x^2) / (2+pi) ]
fy (y) = 4/(2+pi) * [1 - y + radice(1-y^2)]
il punto c) non riesco a capire il dominio. Si dovrebbe intersecare il dominio D con un dominio in cui x>|y| ma graficamente non riesco a vederlo. Mi sono aiutato con wolfram ma non capisco come viene fuori il grafico .-. L'area da calcolare è quella delimitata dal rosso.

Nel secondo esercizio come dovremmo rappresentare la risposta in frequenza? 2*Somma rect( (ni-k)/(0.6) )
Quindi gli impulsi devono essere centrati nei vari k ma essendo a TD, (ni-k) dovrebbe essere un multiplo di 0.6?
Quindi gli impulsi devono essere centrati nei vari k ma essendo a TD, (ni-k) dovrebbe essere un multiplo di 0.6?
Nel secondo esercizio come dovremmo rappresentare la risposta in frequenza? 2*Somma rect( (ni-k)/(0.6) )
Quindi gli impulsi devono essere centrati nei vari k ma essendo a TD, (ni-k) dovrebbe essere un multiplo di 0.6?
citando il libro del prof (capitolo 6.1 - Trasformata di Fourier)
"Bisogna puntualizzare peraltro che, a differenza
delle variabili temporali t ∈ R (caso TC) ed n ∈ Z (caso TD), le variabili frequenziali f e ν variano
entrambi con continuità in R, come evidenziato dal fatto che le equazioni di sintesi sia nel caso TC
che in quello TD sono definite attraverso degli integrali."
bastava rappresentarlo come una finestra rettangolare continua, centrata in 0 e di ampiezza 0.6. Nessun impulso
il punto c) non riesco a capire il dominio. Si dovrebbe intersecare il dominio D con un dominio in cui x>|y| ma graficamente non riesco a vederlo. Mi sono aiutato con wolfram ma non capisco come viene fuori il grafico .-. L'area da calcolare è quella delimitata dal rosso.
Guarda allegato 522
Il dominio è quello. Personalmente l'ho diviso in due domini: un triangolo sopra l'asse delle ascisse e uno "spicchio" sotto l'asse delle ascisse. Si fanno gli integrali sui due domini e si somma il risultato.
Nel punto (b), sei sicuro che la pdf marginale di Y sia quella? Io mi trovo che è pari a:
4/(pi+2)*(1-y) se 0<y<1
4/(pi+2)*rad(1-y^2) se -1<y<0
Il dominio è quello. Personalmente l'ho diviso in due domini: un triangolo sopra l'asse delle ascisse e uno "spicchio" sotto l'asse delle ascisse. Si fanno gli integrali sui due domini e si somma il risultato.
Si purtroppo sono riuscito a capirlo solo dopo, che x > |y| è lo spazio che c'è tra le due bisettrici del primo e quarto quadrante. E intersecando questo col dominio D di partenza, esce fuori quel disegno lì.
Nel punto (b), sei sicuro che la pdf marginale di Y sia quella? Io mi trovo che è pari a:
4/(pi+2)*(1-y) se 0<y<1
4/(pi+2)*rad(1-y^2) se -1<y<0
Altro errore mio. Non avevo tenuto conto del fatto che quando si divide il dominio , si scrivono diverse pdf per diversi valori della variabile. Io invece avevo sommato xD
Posto anche lo svolgimento del 2° esercizio, anche se abbastanza intuitivo.
Si prende il segnale di partenza e lo si sostituisce nel sistema non lineare g(x) al posto della x. Quindi si fa 2 x(n) + x(n) ^ 2.
Qui il trucco sta nello scrivere quel (-1)^n come cos(pi n). [essendo un segnale reale, non c'è la parte "+ jsen (pi n)" ]
quindi abbiamo trovato z(n) che è una somma di coseni a diverse frequenze.
Per y(n) non c'è neanche bisogno di trasformare, basta vedere le frequenze dei coseni di z(n) e scrivere solo quelli che rientrano nella banda passante di H(v) [che è un filtro passa basso tra -0,3 e 0,3 ripetuto con passo 1]
Quindi y(n) sarà qualcosa del tipo: 2 cos (pi n/4) + 3 + 1/2 cos (pi n/2)
[per chiarezza: cos (pi n/4) = cos (2 pi 1/8 n) -> la frequenza è 1/8 = 0,125 che rientra nella banda passante del filtro. Stessa cosa per 1/4= 0,25]
Per la potenza basta ricordarsi che la potenza di un segnale sinusoidale è A^2 / 2, mentre quella della costante k è k^2, quindi
Py = 2 + 9 + 1/8
Si prende il segnale di partenza e lo si sostituisce nel sistema non lineare g(x) al posto della x. Quindi si fa 2 x(n) + x(n) ^ 2.
Qui il trucco sta nello scrivere quel (-1)^n come cos(pi n). [essendo un segnale reale, non c'è la parte "+ jsen (pi n)" ]
quindi abbiamo trovato z(n) che è una somma di coseni a diverse frequenze.
Per y(n) non c'è neanche bisogno di trasformare, basta vedere le frequenze dei coseni di z(n) e scrivere solo quelli che rientrano nella banda passante di H(v) [che è un filtro passa basso tra -0,3 e 0,3 ripetuto con passo 1]
Quindi y(n) sarà qualcosa del tipo: 2 cos (pi n/4) + 3 + 1/2 cos (pi n/2)
[per chiarezza: cos (pi n/4) = cos (2 pi 1/8 n) -> la frequenza è 1/8 = 0,125 che rientra nella banda passante del filtro. Stessa cosa per 1/4= 0,25]
Per la potenza basta ricordarsi che la potenza di un segnale sinusoidale è A^2 / 2, mentre quella della costante k è k^2, quindi
Py = 2 + 9 + 1/8
Sul primo esercizio ho ancora qualche dubbio ma posso dire almeno il primo punto.
Qui abbiamo una risp. impulsiva rappresentata graficamente. Per ricavare la risposta al gradino possiamo usare l'integrale come da definizione, però visto che la funzione è discontinua si divide in diversi integrali, per t<0, [0,T] , [T, 2T] e t>2T
Abbiamo: s(n) = 0 per t < 0.
1/T^2 * [t^2 / 2] per 0 <= t <= T qui c'è un andamento curvo dall'origine fino a T in cui la s(n) assume valore 1/2
1/2 * 1/T * [2t-t] per T <= t <= 2T qui è una retta che parte da T (in cui assume valore 1/2) fino a 2T (in cui vale 3/2)
3/2 t >= 2T e infine procede costante.
per la risposta in frequenza, qui ho delle difficoltà e non mi spingo oltre. [Ho sentito il prof parlare di "teorema di integrazione" ma non ho idea di cosa sia ]
]
Infine per l'uscita y(t) al segnale dato, si può svolgere in frequenza (è un sistema LTI) ricorrendo all'uscita con ingresso un coseno/seno e una costante (che è un fasore a frequenza zero!) e poi antitrasformare.
Chiunque sia riuscito a calcolare H(f), attendo delucidazioni
Qui abbiamo una risp. impulsiva rappresentata graficamente. Per ricavare la risposta al gradino possiamo usare l'integrale come da definizione, però visto che la funzione è discontinua si divide in diversi integrali, per t<0, [0,T] , [T, 2T] e t>2T
Abbiamo: s(n) = 0 per t < 0.
1/T^2 * [t^2 / 2] per 0 <= t <= T qui c'è un andamento curvo dall'origine fino a T in cui la s(n) assume valore 1/2
1/2 * 1/T * [2t-t] per T <= t <= 2T qui è una retta che parte da T (in cui assume valore 1/2) fino a 2T (in cui vale 3/2)
3/2 t >= 2T e infine procede costante.
per la risposta in frequenza, qui ho delle difficoltà e non mi spingo oltre. [Ho sentito il prof parlare di "teorema di integrazione" ma non ho idea di cosa sia
Infine per l'uscita y(t) al segnale dato, si può svolgere in frequenza (è un sistema LTI) ricorrendo all'uscita con ingresso un coseno/seno e una costante (che è un fasore a frequenza zero!) e poi antitrasformare.
Chiunque sia riuscito a calcolare H(f), attendo delucidazioni
Per y(n) non c'è neanche bisogno di trasformare, basta vedere le frequenze dei coseni di z(n) e scrivere solo quelli che rientrano nella banda passante di H(v) [che è un filtro passa basso tra -0,3 e 0,3 ripetuto con passo 1]
Quindi y(n) sarà qualcosa del tipo: 2 cos (pi n/4) + 3 + 1/2 cos (pi n/2)
[per chiarezza: cos (pi n/4) = cos (2 pi 1/8 n) -> la frequenza è 1/8 = 0,125 che rientra nella banda passante del filtro. Stessa cosa per 1/4= 0,25]
Il ragionamento è quello, anche se bisogna fare attenzione perché ci sono dei coseni al quadrato e la frequenza cambia. Trasformare tutto è molto lungo e laborioso, ma aiuta.
per la risposta in frequenza, qui ho delle difficoltà e non mi spingo oltre. [Ho sentito il prof parlare di "teorema di integrazione" ma non ho idea di cosa sia]
Chiunque sia riuscito a calcolare H(f), attendo delucidazioni
Io mi sono avventurato nel calcolarla come la trasformata di Fourier di una rampa tra 0 e T (applicando la definizione) e la trasformata di Fourier di una porta tra T e 2T, ma non so se è corretto. La funzione finale che mi esce fuori presenta una f al denominatore, per cui per calcolare il valore per f = 0 si deve fare un limite. Magari è corretto, ma ho la sensazione che ci dev'essere qualche modo più veloce.
Non ho idea di quale sia il teorema al quale si riferisce il professore...dove l'hai sentito?
Ragazzi scusate i tempi.. Per quanto riguarda il 3.2) qualcuno saprebbe dirmi come fare a rappresentare graficamente e verificare la validità delle pdf marginali?
- Per il grafico ci si riesce semplicemente andando a sostituire dei valori ad x e y?
- Per la validità ho cercato di verificare la proprietà di area unitaria ma ho difficoltà nello scegliere gli estremi di integrazione..
Se qualcuno potesse illuminarmi mi farebbe un grosso favore!
- Per il grafico ci si riesce semplicemente andando a sostituire dei valori ad x e y?
- Per la validità ho cercato di verificare la proprietà di area unitaria ma ho difficoltà nello scegliere gli estremi di integrazione..
Se qualcuno potesse illuminarmi mi farebbe un grosso favore!
Ultima modifica:


